Actividad dedicada al profesor Antonio F. Costa, por su cumpleaños (del 31 de mayo de 2017
En el vídeo mostramos cómo construir el famoso bonete cruzado con papel. Para los topólogos el bonete cruzado es muy interesante pues se trata de un modelo de la cinta de Moebius que puede taparse con un disco para obtener el bonete cruzado (cerrado), un modelo del plano proyectivo en R^3. Dicho modelo contiene un segmento de puntos dobles y dos puntos singulares.
Este modelo del bonete cruzado tiene la ventaja de ser simétrico (si se se construye con una hoja más estrecha se aprecia mejor; véase foto abajo).
Lo que no mostramos en el vídeo es el experimento de cortar una cinta por su mitad, ¿te animas? ¿Qué crees que saldrá al cortar este modelo? ¡Te sorprenderá! ¿y si lo cortas por 1/4? Es interesante comparar los resultados con los que se obtienen con una cinta de Moebius estándar.
Para construir este modelo de papel, me he inspirado en una animación magnífica de Jos Leys [Leys 2].
Cross-cap with paper
The video shows how to build the famous (open) cross-cap with paper. The cross-cap is very interesting to topologists, as it is a model of the Moebius strip which can be closed with a disc, to obtain the closed cross-cap, a model of the projective plane in R^3. This contains a segment of double points, and 2 singular points.
This model is symmetric (for that better start with a narrower sheet; see picture below).
What I haven’t show in the video is the experiment of cutting the Moebius strip by half, would you like to try? You will be surprised! What about cutting it by 1/4? It is interesting to compare the results with same experiments with the standard Moebius strip.
Our paper model was inspired by an animated video of Jos Leys [Leys 2].

La figura anterior es un modelo de cartulina de la superficie de Plücker:
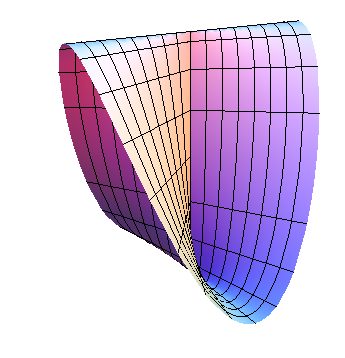
Mathematica: ParametricPlot3D[{v Cos[u], v Sin[u], Sin[2 u]}, {u, 0, Pi}, {v, -1,1}]
Otra versión casi igual es la «Wallis’s conical edge»

ParametricPlot3D[{v Cos[u], v Sin[u], Sin[2 u]}, {u, 0, Pi}, {v, -1, 1}]
Bonete cruzado de fieltro
¿Y si realizamos el mismo modelo con fieltro? En tal caso, se pueden coser las costuras para cerrarlo (excepto la línea de puntos dobles) y obtener un modelo del bonete cruzado cerrado (es decir, del plano proyectivo). El resultado se muestra en el siguiente video: una funda matemática muy interesante y curiosa que sirve para guardar nuestro móvil, y de la que incluso podemos sacar dinero, sabiendo que el plano proyectivo vive en la 4ª dimensión, ¡claro!
Referencias/references:
- https://en.wikipedia.org/wiki/Cross-cap
- https://topologia.wordpress.com/2008/12/25/5-el-plano-proyectivo-y-la-cinta-de-mobius/
- [Leys] https://www.youtube.com/watch?v=u0VkikpElMo
- [Leys1] https://www.youtube.com/watch?v=yeaw3BnCs34
- [Leys 2] https://www.youtube.com/watch?v=W-sKLN0VBkk
Esta entrada participa en la Edición 8.4 “Matemáticas de todos y para todos” del Carnaval de Matemáticas cuyo anfitrión es, en esta ocasión, matematicascercanas

2 replies to “Bonete cruzado con papel”